Does your math curriculum include ballpark estimates? Or perhaps rounding? My school uses Everyday Math and in the spring we have to teach ballpark estimates. However, it’s so confusing because it is really adding rounded numbers to get an estimate – like you do at the grocery store: “The milk is $3.79 and the cereal is $4.99 so that’s about $4 and $5 . $4 + $5 = $9. I have a $10 bill so I am all set.”
Well don’t get stressed because I have some tips for you math teachers!
First, to make sense of why we are teaching this, think about real life situations like the shopping example above, but also consider that the traditional double digit addition and subtraction with regrouping algorithms are not expected of students in the common core until fourth grade. YES, fourth grade*. However, third graders and even second graders need to be able to add and subtraction double digits according the the common core state standards.
*yes, the algorithm is first mentioned in third grade but as an strategy for students to solve two and three digit addition to 1,000. Students are not expected to master it (be fluent) until the end of fourth grade.
For example, in grade two:
2.NBT.B.5
Fluently add and subtract within 100 using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction.
2.NBT.B.6
Add up to four two-digit numbers using strategies based on place value and properties of operations.
And in grade three:
3.NBT.A.1
Use place value understanding to round whole numbers or the nearest 10 or 100.
3.NBT.A.2
Fluently add and subtract within 1000 using strategies and algorithms based on place value, properties of operations, and/or the relationship between addition and subtraction.
So what is all that “using strategies based on place value, properties of operations, and/or the relationship between addition and subtraction”? Well, strategies are key! And rounding numbers to then add or subtract is a strategy. I suppose it goes mostly within the place value domain, because students have to know what tens or hundreds number it is near.
For example, a student is give the number 21 and 39 and directed to make a ballpark estimate. They first must know 21 is between the benchmark numbers 20 and 30, but closer to 21, and 39 is between 30 and 40 but closer to 40.
So 21 + 39 =?
becomes
20 + 40 = 60!
So students need to learn rounding first. Greg Tang, one of my all time favorite math presenters, says to not worry about rhymes and mnemonics with your students (such as “1-4 , hit the floor, 5-9 climb the vine”). He, and many other mathematicians, say use teachers should implement number lines – especially open number lines.
Students need to first determine the benchmark numbers. For example, if you are rounding 23 to the nearest 10, they are 20 and 30. Students then would use the open number line (I love white boards for this but sometimes you just grab a piece of paper), to place the number they need to round in the middle (such as 23). Then if they need a visual, they would write in the nearby numbers (20-30) , evenly spaced, so that they can see which benchmark number is closest to 23.


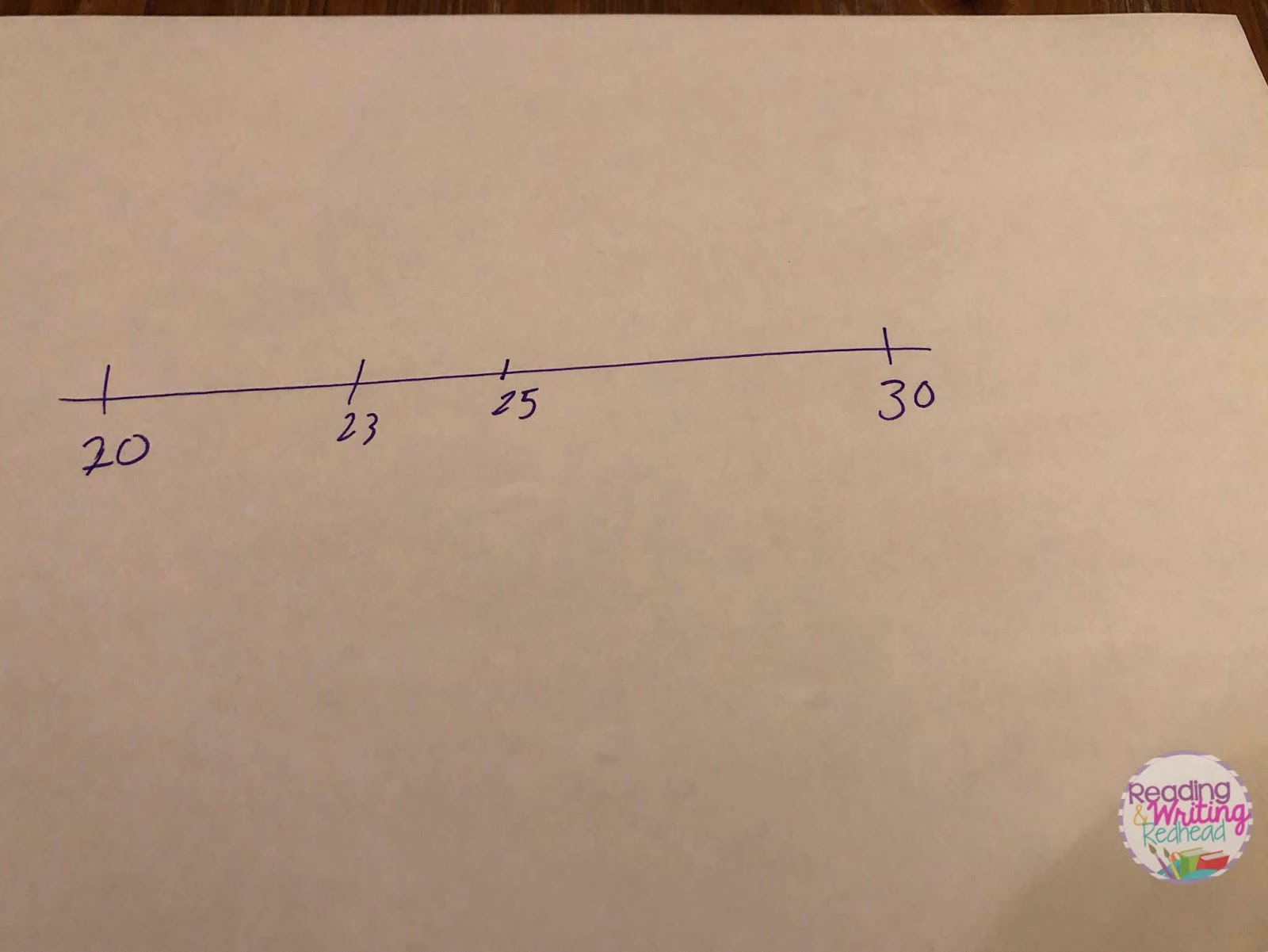
The Recovering Traditionalist has a lot more details at her blog post, How to Teach Rounding Numbers. I also love Greg’s (Mr. Elementary Math’s advice too) at his blog.
Looking for resources?
This is a very detailed poster available from Amazon (click to see) on rounding – perhaps best for older students.
A simpler free poster download (you have to print) from JJ Resource Creation.
Free rounding practice pages that accompany their Rounding Posters from Really Good Stuff.
Numberock does have premium content but this Rounding whole Numbers video was free to watch. Might be better for 4th grade and up!

The Ballpark Estimate pack includes these activities:
- Background information for teachers
- Ballpark estimate mini posters for classroom
- Cut and glue two digit addition with ballpark estimates – addition
- Cut and glue two digit addition with ballpark estimates – addition
- Five ballpark estimate practice pages addition and subtraction with answers



What is your favorite tip or strategy for teaching ballpark estimates? Let us know!